Стационарные точки
Все стационарные точки находятся так, как корни уравнения
Если функция Nt является неотрицательной, то имеют смысл
только неотрицательные корни уравнения (3).
Решение уравнения (1) можно наглядно продемонстрировать с помощью диаграммы и
лестницы Ламерея (рис.1) Абсциссы точек пересечения биссектрисы первой четверти
координатной плоскости (N,y) определяют равновесные состояния. На рис. 1А)
показан способ нахождения значений Nt в последовательные моменты времени. Пусть в
начальный момент t = 0 имеем N = N0, тогда F(N0) = N1
задает значение N в момент времени t = 1. Величина N1, в свою очередь, определяет
значение F(N1) = N2. И так далее. На рис. 1Б) приведен пример, когда
числовая последовательность - траектория развития популяции - сходится к равновесному состоянию, совершая
затухающие колебания.
Стационарное решение Nt = N*, t = 0,1,2,..., называется устойчивым, если
для любого ε > 0 существует δ > 0 такое, что
Если
 , |
то решение Nt = N*, t = 0,1,2,..., называют
асимптотически устойчивым.
Аналитический критерий исследования на асимптотическую устойчивость
Рассмотрим случай локальной асимптотической устойчивости.
Рассмотрим уравнение (1) в произвольной окрестности положения равновесия - N*.
Построим для уравнения (1) соответствующее линеаризованное. Для этого рассматриваем
(1) в окрестности точки покоя N*. Линеаризовать необходимо только правую часть; раскладываем
в ряд Тейлора, сохраняя только линейную часть:
 , |
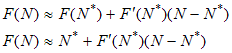Таким образом, в окрестности точки N* можно записать:
 , |
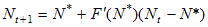Обозначим xt = Nt - N* - отклонение от положения равновесия
в момент времени t, тогда
 , |
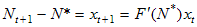- динамика отклонений.
Это уравнение определяет геометрическую прогрессию со знаменателем F′(N*), т.е.
Возможны несколько случаев:
Если F′(N*) < -1, то N* - неусточиво; траектория совершает колбания с нарастающей апмлитудой.
Если |F′(N*)| = 1 или F′(N*) = 0 , то по поведению решения соответствующего линеаризованного уравнения нельзя сделать вывод об устойчивости положения равновесия и требуются дополнительные исследования.
Если -1 < F′(N*) < 0, то N* - асимптотически устойчиво, отклонения затухают, а траектория совершает затухающие колебания.
Если 0 < F′(N*) < 1, то N* - асимптотически устойчиво, отклонения монотонно затухают.
Если F′(N*) > 1, то N* - неустойчиво, причем имеет место монотонное нарастание отклонений.
Уравнение (1) всегда имеет нулевое положение равновесия. Остальные положения - необязательно.
Циклы
При анализе уравнения (1) кроме иммледования стационарных решений выясняют наличие и характер устойчивости периодических решений (циклов).
Решение {Nt*}|t = 0,1,2,...
уравнения (1), состоящее из конечного набора T (T > 1) значений, повторяющихся в строгой последовательности, т.е. когда:
называют циклом длины Т (или T-точечным циклом, или просто Т-циклом).
Цикл длины Т будем записывать следующим образом:
Точки 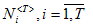 , образующие цикл, являются решением следующей системы:
Очевидно, что они находятся среди корней уравнения:
Рассмотрим случай, когда требуется найти циклы длины T = 2, т.е. существует числовая
последовательность со следующим свойством:
Значит:
| (4) |
 . |
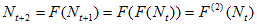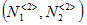 - цикл длины 2. Точки,образующие цикл, определяются следующим образом:
| (5) |
 . |
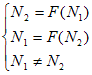Если система (5) имеет решение, то уравнение (1) имеет цикл длины 2:
| (6) |
 . |
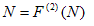Среди решений уравнения (6) есть равновесные точки. Решив (6), необходимо исключить все точки покоя. Оставшиеся точки образуют цикл. Если ничего не останется, то циклов нет.
Рассмотрим понятие устойчивости для циклов. Числовая последовательность, рассматриваемая с шагом по времени равным 2, дает нам 2 числовые последовательности: N1, N1, N1,... и N2, N2, N2,..., каждая из которых является стационарным решением уравнения (4), рассматриваемого с шагом по времени равным 2. Устойчивость цикла длины 2 зависит от устойчивости точек N1, N2, как равновесных. Т.о. N1 будет асимптотически устойчиво, если выполняется неравенство:
 . |
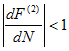Преобразуем его:
 . |
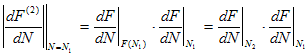Это выражение должно быть по модулю меньше 1. Аналогично для N2. При этом цикл является притягивающей траекторией, т.е. устойчивым. Если полученное выражение по модулю меньше 1, то цикл называют отталкивающим; если равно 1, то нейтральным.
Критерий асимптотической устойчивости для цикла длины T: цикл 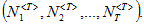 называют притягивающим, отталкивающим или нейтральным, если соответственно:
 . |
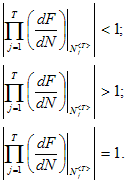Наряду с равновесием и циклами можно выделить еще один тип поведения решения разностного уравнения (1). Это так называемые хаотические траектории, т.е. непериодические последовательности {Nt}t=0,1,..., и даже, более того, не стремящиеся ни к какому притягивающему равновесию или циклу. Существует связь между наличием цикла периода 3 и существованием хаотических решений.
Теорема. Если уравнение (1) обладает трехточечным циклом, то оно имеет также и решение любого периода и, кроме того, существует несчетное множество начальных значений N0, при которых решение не стремится ни к одному из этих циклов, т.е. хаотично [3, 4].
|
