Исследуем модель. Построим уравнения, в которых не будет F.

Умножим первое уравнение на γ₂, второе - на γ₁ и вычтем из первого второе.

(3)

Подчиним начальным условиям:

Будем предполагать, что

(4)

Сформулируем свойства функции F, которыми будем пользоваться при дальнейшем анализе:

F = 0, если N₁ = N₂ = 0.

F > 0 для любых N₁, N₂ > 0

При неограниченном возрастании N₁ и N₂ F тоже неограниченно возрастает.

F монотонно возрастает по каждому своему аргументу:

Пусть N₁^* - корень уравнения

В момент, когда достигается численность первого вида, равная N₁^*, численность второго вида равна N₂. Может ли N₁ увеличиваться дальше?

Значит, не может. Значит, N₁ - ограниченная функция. Аналогично, N₂ - ограниченная. Следовательно, невозможен неограниченный рост численности.
Правая часть (3) стремится к бесконечности в силу (4). Левая часть - отношение двух ограниченных функций, значит, знаменатель стремится к нулю, т.е. первый вид вытесняет второй.

Положения равновесия

Решение системы (1) вида

называется стационарным решением. (N₁^*, N₂^*) - положение равновесия. Найдем их из решений системы

Система распадается на 4 системы:
1. N₁^* = N₂^* = 0. Обозначим эту точку покоя - P₀(0 ,0).
2. N₁^* = 0, N₂^*:

(5)

В силу монотонности решение (5) существует всегда. Значит, вторая точка покоя - P₁(0, N₂^*), где N₂^* - корень уравнения (5).
3. N₂^* = 0, N₁^*:

(6)

Тоже всегда есть решение. Точка покоя - P₂(N₁^*, 0), где N₁^* - корень уравнения (6).

Вывод: система (1) имеет три точки покоя.

Характер устойчивости

Исследование на асимптотическую устойчивость проведем с помощью линеаризации. Рассмотрим построение линеаризованной системы для (1) в окрестности произвольного положения равновесия P^*.
Правые части (1) необходимо заменить линеаризованными функциями:

Аналогично для правой второго уравнения системы (1).
Получаем:

Отклонение от положения равновесия по соответствующей координате:

Линеаризованная система имеет вид:

(7)

Итак, имеем три точки покоя и линеаризованную систему (7). Исследуем на устойчивость каждую точку отдельно.
Первая точка покоя. P₀(0, 0). Подставляя в (7), получаем:

Решение:

x₀, y₀ - начальное отклонение. Точка P₀ неустойчива, малые отклонения от положения равновесия со временем нарастают. Т.к. собственные значения системы

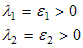то P₀ - неустойчивый узел.
Вторая точка покоя. P₁(0, N₂^*). Соответствующая линеаризованная система:

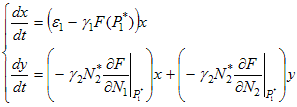Матрица системы имеет треугольный вид, значит собственные значения совпадают с коэффициентами главной диагонали:

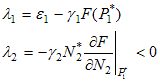Определим знак первого собственного значения λ₁:

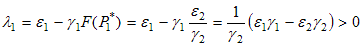Получили, что собственные значения имеют разный знак. P₁ - "седло". "Седло" всегда неустойчиво.
У "седла" две сепаратрисы - прямые, найдем их. Будем искать в виде: y = kx.

Выразим k₁:

Числитель дроби отрицателен, знаменатель положителен. Значит k₁ < 0. Нашли только одно конечное значение k, значит

Получаем две сепаратрисы:

Сепаратрисы разбивают фазовую плоскость на 4 области. Вся плоскость заполняется траекториями. Как определить направление движения по траектории? Пусть x = 0, как изменится y? Подставим x = 0 во второе уравнение. Получим решением экспоненциальную функцию, стремящуюся к нулю. Значит y убывает.

Третья точка покоя. P₂(N₁^*, 0). Соответствующая линеаризованная система имеет вид:

Матрица системы имеет треугольный вид. Ниже главной диагонали - нули, значит, собственные значения системы имеют вид:

Получаем, что собственные значения вещественны и отрицательны. Значит, P₂ - устойчивый узел.

Первый вид (если он есть) вытесняет второй. Количество особей первого вида стремится к некоторой константе. Чем больше величина ε/γ, тем меньше нехватка пищи сказывается на поведении особей. В нашем случае

Условие (4) может быть нарушено. Например, ε₁γ₂ - γ₁ε₂ < 0, но это тоже самое, что изменить нумерацию видов. Ничего не изменится, только второй вид, наоборот, будет вытеснять первый.
Рассмотрим случай, когда ε₁γ₂ = γ₁ε₂, т.е. оба вида реагируют на нехватку пищи одинаково. Изменится соотношение (3):

- уравнение фазовой траектории.
Вспомним, как мы искали положения равновесия. Четвертый случай был

- это целая линия точек.
Рассмотрим случай, когда F(N₁, N₂) = N₁ + N₂. Эта функция удовлетворяет условиям.

Нулевое положение так и останется неустойчивым. Весь отрезок состоит из устойчивых точек, но нет асимптотической устойчивости.
Пересечение вертикальных и горизонтальных изоклин дает точку покоя. Вертикальные изоклины найдем из условия N₁^* = 0, горизонтальные - N₂^* = 0:

Если F = N₁ + N₂, то